LCM and HCF | Fractions and Decimal questions | HCF division method

How to find LCM and HCF of simple problems, fraction, decimal and many more. LCM and HCF questions are covered in-depth along with examples and figures. 

HCF full form - Highest common factor:

• HCF definition - HCF is the largest number which divides the given numbers exactly
• HCF is always less than or equal to the smallest of the given numbers

Example: HCF of 4, 6, 8 and 10 is 2, because 2 is the largest number, which divides 4, 6, 8 and 10 exactly. Readers also must notice that HCF is lesser than the smallest of the given numbers.

LCM full form - Lowest common multiple:

• LCM definition - LCM is the smallest number that is divisible by all given numbers.
• LCM is always greater than or equal to the largest of the given numbers.

Example: LCM of 4, 6, 8 and 10 is 120 because 120 is the smallest number, which is divisible by the 4, 6, 8 and 10 exactly.

Now we know the full form of LCm and HCF along with their definition, now let's see how to find LCM and HCF. 

How to find HCF:

For HCF there are 2 methods:

1. Factor method
2. Division method.

As we will proceed, I will teach you some technique from which you will be able to solve LCM and HCF problems in few seconds in your mind without even using pen and paper. But before that, it is important to know basic methods.

• Factor method: List all the prime factors of all the number and then find the factors which are common to every number.

Example: Find HCF of 4 and 6.

HCF of two numbers

HCF of two numbers

It is clear that '2' is the only common factor in the factors of 4 and 6.

So, HCF of 4 & 6 = 2

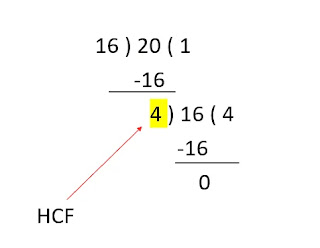
• How to find HCF by Division method: 

Find HCF of 4 & 6

HCF division method

Step 1: Divide the larger number by the smaller number. 

Step 2: Find the remainder. If the remainder comes out to be zero the divisor itself become the HCF of them but if remainder does not come equal to zero, the remainder becomes new divisor and divisor of the previous step become dividend. Again find reminder if it comes to zero the divisor of 2nd step become HCF otherwise the process will continue until reminder becomes zero.

In this example 4 is the smaller number while 6 is the larger. So, 6 become the dividend and 4 become divisor. After dividing 6 by 4 remainder comes out to be 2. now 2 become divisor and 4 become dividend and remainder turns out to be zero. So, 2 become the HCF.

How to find LCM: 

To find the LCM of the given numbers divides all the numbers at the same time by a prime number. Generally, it is suggested to start from smallest prime number that is 2, if any number is exactly divisible by 2, divide those number by '2' and write remaining numbers itself below the line.

If any number is again exactly divisible by 2 divides that no. by '2' and continue to write non-divisible numbers as it is below the line. Once it is confirmed that no number is now divisible by '2' now check for next prime number 3 and follow the same procedure. This procedure continues until '1' appears below every number. 

How to find LCM

Let’s solve few more examples:

Find LCM and HCF of 16, 20 and 36.

HCF using division method:

HCF of 16, 20 and 36 

Step 1: First choose any two numbers. let I choose 16 and 20

Step 2: Find the HCF of those two numbers. In this example, it is 4.

Step 3: Now Find HCF of the third number and the HCF of the first two numbers. In this example, HCF of 4 ( HCF coming from first two numbers ) and 36 (Third number) is 4.  

Step 4: HCF coming from step 3 become the final HCF of all three numbers. 

HCF of 16, 20 and 36 = 4

HCF by division method

HCF of three numbers by division method

HCF Using factor method:

HCF of three numbers by factor method

LCM of 16, 20 and 36: 

Step 1: Write all the Prime factors of every number. Write those factors in terms of power. 

In this example, 16 can be written as 24

  

Step 2: List all the factors which are appearing in those numbers. Write down each factor with the highest power and multiply them to find LCM.

In this example 2, 3, and 5 are appearing. The highest power of 2, 3 and 5 are 4, 2 and 1 respectively. 

So, LCM is 24 * 32 * 5 = 720

LCM of three numbers

Find LCM of 10, 15 and 25. 

LCM of three numbers

H.C.F. and L.C.M. of Fractions:

HCF =	HCF of Numerators
	LCM of Denominators

LCM =	LCM of Numerators
	HCF of Denominators

Example: Find LCM and HCF of 2/3, 5/6, 3/2 

LCM =	LCM of 2, 5 and 3
	HCF of 3, 6 and 2

LCM. of 2, 5 and 3 is equal to 30

& HCF of  3, 6 and 2 is equal to 1

LCM of 2/3, 5/6, 3/2 

= 30/1 = 30

                                                                                                                                                                   

HCF =	HCF of 2, 5 & 3
	LCM of 3, 6 & 2

HCF of 2, 5 and 3 is equal to 1
& LCM of  3, 6 and 2 is equal to 6

LCM of 2/3, 5/6, 3/2 

= 1/6 

LCM and HCF of decimal numbers:

Example: Find LCM and HCF of 0.1, 0.15 and 0.25

1. To solve such type of questions first convert decimal numbers into integers.
2. To convert them on integer we must multiply all the numbers by the same number so that all of them convert into integers.
3. In this example, Multiplying by 100 to all numbers the number becomes 10, 15 and 25.
4. LCM of 10, 15 and 25 can be found easily.
5. Because we initially multiply the decimal numbers by 100 to convert them on integer. After getting LCM of integers we must divide that by 100 so that we get the answer to our original problem.

LCM of 0.1, 0.15 and 0.25 = 

LCM. =	LCM of 10, 15 and 25
	100

 = 150/100 = 1.5

HCF of 0.1, 0.15 and 0.25 =

HCF =	HCF of 10, 15 and 25
	100

= 5/100 = 0.05

Find LCM and HCF of the 31, 32, 33, 34, 35

Readers must notice that in this example base are same, but the exponents are different.

In these type of questions, LCM is the number which is raised to the highest power while HCF is the number raised to the lowest power.

• HCF = 31= 3
• LCM = 35  = 243

Find LCM and HCF of the 3-1, 3-2, 3-3, 3-4, 3-5

This question is based on a similar concept explained in the above example 

• LCM = 3-1
• HCF = 3-5

Tab: LCM and HCF, How to find LCM, How to find HCF questions

So, Friends tell me in comments about how you find this article your feedback is  important and tell me your problems , I am always here for you.......

Also, do not forget to like, share and follow this post.......