Types of numbers | Rational numbers | Irrational numbers

Know all 11 types of numbers in-depth along with examples. These are always asked in school exams, competitive exams, and interviews.

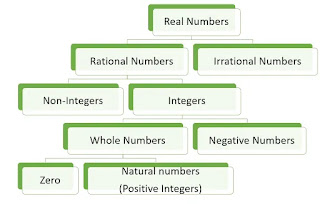
Types of Numbers:

• Real Number
• Rational Number
• Irrational Number
• Integers
• Whole Number
• Natural Number
• Prime Number
• Composite Number
• Even Number 
• Odd number
• Complete Number

Type of numbers

Real Number: 

Real number is any number (Positive, Negative or Zero) that includes all the rational and irrational numbers.

Example: 1, 2.2684654, π, 8/3 etc

A real number always can be found on the number line. These are the numbers we use in real-world applications.

Rational Number: 

A number which can be written in the form of P/q, where both P and q are integers and q is not equal to zero.

• All the fractions are rational numbers. For example 3/8 
• Integers are rational numbers. For example, 6 is a rational number because it can be written as 6/1
• All the decimal numbers terminated after a few decimal points are rational numbers.      Example 2.15, 216.3698                                                                                                                   
• All the decimal numbers which do not terminate but its digits are repeating in nature are also rational numbers.                                                                                             
• For example - 3.333333333.......... And 0.714285714285……….                                          
• In 3.3333333, 3 is not terminated but it gets repeated, so it is a rational number. It can be written as 10/3.                                                                                                                    
• In 0.714285714285, 714285 continuously gets repeated so it is also a rational number and it can be written as 5/7.

Irrational numbers: 

These numbers can not be written in the form of p/q.

Π is an irrational number, where Π = 3.141592654…….

Π is irrational because neither it is terminating nor repeating in nature.

Integers: 

An integer is a number that can be written without a fractional component. In other words, an integer has denominator equal to 1.

Example: -20, 0, 516

Whole Numbers: 

These are the numbers which contain zero and positive integers.

Example: 0, 13, 150

Natural numbers:  

Positive integers are known as a natural number. Zero is not a natural number. So if we remove zero from the list of whole numbers we get the natural number.

Example: 1, 1234, 23246

Prime numbers:

A prime number is a number is only divisible by 1 and itself.

Example: 2, 3, 5, 7, 11

• 1 is not a prime number
• 2 is the smallest prime number
• Also, 2 is only even prime number

Composite numbers: 

All the positive integers other than prime numbers are composite numbers.

Example: 4, 6, 8, 9, 10, 12

• 1 is neither prime nor composite.

Even numbers:

Those numbers which are divisible by 2 are even numbers, in other words, the numbers whose unit digit is 0, 2, 4, 6 or 8 are even numbers.

Example: 28, 226

Odd numbers:

Those numbers which are not divisible by 2 are called odd numbers, in other words, the numbers whose unit digit is 1, 3, 5, 7, 9 are called odd numbers.

Example: 21, 233

Complete number: 

A positive number is said to be complete if the sum of all positive divisors of the number is equal to the twice of the number itself.

Example: 6, 28

• Divisor of 6 are 1, 2, 3 and 6

1 + 2 + 3 + 6 = 12, which is the twice of 6, So 6 is a complete number

• Divisor of 28 are 1, 2, 4, 7, 14, 28

1 + 2 + 4 + 7 + 14 + 28 = 56, which is twice of 28 so 56 is a complete number.

  

If you like this article, Please like, share and follow my blog

If you have any doubt you can ask on comment section................